简要介绍SVM
支持向量机，因其英文名为support vector machine，故一般简称SVM，通俗来讲，它是一种二分类模型，基本模型定义为特征空间上的间隔最大的线性分类器，学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。其中支持向量是满足$|w^Tx+b|=1$的点，除了支持向量外所有的点满足$y|w^Tx+b|>=1$。这种方式得到的模型能够用来处理线性的情况，通过引入核函数将扩展到非线性情况下。
事实上，大部分时候数据并不是线性可分的，这个时候满足这样条件的超平面就根本不存在。在上文中，我们已经了解到了SVM处理线性可分的情况，那对于非线性的数据SVM咋处理呢？对于非线性的情况，SVM 的处理方法是选择一个核函数，通过将数据映射到高维空间，来解决在原始空间中线性不可分的问题。 具体来说，在线性不可分的情况下，支持向量机首先在低维空间中完成计算，然后通过核函数将输入空间映射到高维特征空间，最终在高维特征空间中构造出最优分离超平面，从而把平面上本身不好分的非线性数据分开。
核函数将原先的公式用非线性变换$\phi$转换，首先使用一个非线性映射将数据变换到一个特征空间F，然后在特征空间使用线性学习器分类。 $$f(x,y)=w^Tx+b$$ $$f(x,y)=w^T\phi(x)+b$$
常用核函数：
- 多项式核函数
$$k(x_1,x_2)=(
上述证明都是基于不存在outilers的情况下，但是实际过程中，在最大间隔间中存在outilers，此时引入松弛变量来处理，也就是酱outilers中的点也加入到Loss中，其中C为松弛变量。
主要构造不等式约束的拉格朗日乘子法，然后用对偶方式将minmax转换为maxmin的方式进行求解。
拉格朗日乘子法、KKT条件 拉格朗日乘子法：
单一等式约束的拉格朗日乘子法：
$$min_{(x, y)}{f(x,y)}$$ $$s.t.\ g(x,y)=c$$
表示最优化满足如下条件：
$$\nabla f(x,y)=\lambda \nabla (g(x,y)-c)$$
即最优化点满足两个函数的法向量相同，如下构造拉格朗日乘子：
$$L(x,y,\lambda)=f(x,y)+\lambda (g(x,y)-c)$$
多个等式约束的拉格朗日乘子法
将单一等式约束的拉格朗日乘子法扩展即可： $$min{(x, y)}{f(x,y)}$$ $$s.t.\ g{i}(x,y)=0, i=1,2,…,N$$ $$L(x,y,\lambda)=f(x,y)+\sum{i=1}^{N}{\lambda{i} g_{i}(x,y)}$$
广义拉格朗日乘子法
$$min{(x, y)}{f(x,y)}$$ $$s.t.\ g{i}(x,y)=0, i=1,2,…,N$$ $$h{i}(x,y)<=0, i=1,2,…,M$$ 构造广义拉格朗日乘子法 $$L(x,y,\alpha,\beta)=f(x,y)+\sum{i=1}^{N}{\alpha{i} g{i}(x,y)}+\sum{i=1}^{M}{\beta{i} h{i}(x,y)}$$ 满足如下KKT条件即可求得最优解： - 法向量相同 $$\nabla L(x,y,\alpha,\beta)=0$$ - 基本条件 $$g{i}(x,y)=0, i=1,2,…,N$$ $$h_{i}(x,y)<=0, i=1,2,…,M$$ - 不等约束系数非负 $$\beta_i>=0, i=1,2,…,M$$ - 不等约束和系数其中一个为0 $$\beta_i h_i(x,y)=0, i=1,2,…,M$$
对偶和KKT条件 对偶和KKT条件 《SVM笔记系列之三》拉格朗日乘数法和KKT条件的直观解释 这篇文章对理解拉格朗日乘子法帮助很大 拉格朗日乘数
支持向量机通俗导论（理解SVM的三层境界） 解密SVM系列（一）：关于拉格朗日乘子法和KKT条件
请简要介绍下tensorflow的计算图
2015百度校招机器学习题目
关于LR逻辑回归
逻辑回归
@rickjin：把LR从头到脚都给讲一遍。建模，现场数学推导，每种解法的原理，正则化，LR和maxent模型啥关系，lr为啥比线性回归好。有不少会背答案的人，问逻辑细节就糊涂了。原理都会? 那就问工程，并行化怎么做，有几种并行化方式，读过哪些开源的实现。还会，那就准备收了吧，顺便逼问LR模型发展历史。
虽然逻辑回归（Logistic Regression）称为回归，不过其实它的真实身份是二分类器，这个名字来源于逻辑斯蒂分布，回归将式子回归到[0,1]，而分类则如果大于0则为正样本，如果小于0则为负样本。
$$z=w^Tx+b$$
$$ y=\left{
\begin{array}{rcl}
0 & & {z < 0}
0.5 & & {z = 0}
1 & & {z > 0}
\end{array} \right. $$
$$y=\frac{1}{1+e^{-z}}$$ $$y=\frac{1}{1+e^{-(w^Tx+b)}}$$ 其中$\ln{\frac{y}{1-y}}$称为对数几率 $$\ln{\frac{y}{1-y}}=w^Tx+b$$
逻辑回归BP推导
令$h_w(x)=\frac{1}{1+e^{-w^T x}}$，其中$w=(w_0, w_1, \cdots, w_d)^T$，$x=(1, x^1, \cdots, x^d)^T$，$X=(x_1, x_2, \cdots, x_N)$，共有$N$个样本，$d$维特征，$LR$中的$Sigmoid$函数导数$h_w(x)^{\prime}=h_w(x)(1-hw(x))$。其中代价函数如下所示： $J(w)=-\frac{1}{N}\sum{i=1}^{N}(y_i \log h_w(x_i)+(1-y_i) \log (1-h_w(x_i)))$ $\frac{\partial{J(w)}}{wj}=-\frac{1}{N}\sum{i=1}^{N}(y_i \frac{1}{ h_w(x_i)}-(1-y_i) \frac{1}{(1-h_w(x_i))})\frac{\partial{h_w(x_i)}}{\partial{wj}}$ $=-\frac{1}{N}\sum{i=1}^{N}(y_i \frac{1}{ h_w(x_i)}-(1-y_i) \frac{1}{(1-h_w(x_i))})h_w(x_i)(1-h_w(w_i))\frac{\partial{w^T x}}{\partial{wj}}$ $=-\frac{1}{N}\sum{i=1}^{N}(y_i \frac{1}{ h_w(x_i)}-(1-y_i) \frac{1}{(1-h_w(x_i))})h_w(x_i)(1-h_w(w_i))xi^j$ $=-\frac{1}{N}\sum{i=1}^{N}(y_i (1-h_w(x_i))-(1-y_i) h_w(x_i))xi^j$ $=-\frac{1}{N}\sum{i=1}^{N}(y_i - h_w(x_i))xi^j$ $=\frac{1}{N}\sum{i=1}^{N}(h_w(x_i)-y_i)x_i^j$ 使用梯度下降算法更新： $w_j=wj-\alpha \frac{1}{N}\sum{i=1}^{N}(h_w(x_i)-y_i)x_i^j$ 矩阵形式为： $w=w-\alpha \frac{1}{N}X^T(h_w(X)-y)$
逻辑回归（LR）总结复习 推导主要参考这个博客。
逻辑回归原理小结 刘建平的博客，依旧是参考的重点。
逻辑回归的正则化
正则化是符合奥卡姆剃刀(Occam’s razor)原理的：在所有可能选择的模型中，能够很好地解释已知数据并且十分简单的才是最好的模型。正则化项是为了防止模型容量大，而数据样本小，从而导致模型将不属于泛化特征而属于训练集本身的特征学习到了，从而虽然在训练集上表现较好但是在测试集上表现极差，即泛化能力降低，产生过拟合。正则化通过增加对某种表达式的偏好程度来减小模型的复杂度，从而达到简单化同时泛化能力强的效果，常用的正则化有L1正则化、L2正则化
L1正则化和L2正则化可以看做是损失函数的惩罚项。所谓『惩罚』是指对损失函数中的某些参数做一些限制。对于线性回归模型，使用L1正则化的模型叫做Lasso回归，使用L2正则化的模型叫做Ridge回归（岭回归）。 - L1正则化 L1正则化是指权值向量w中各个元素的绝对值之和，通常表示为$||w||_1$ L1正则化可以产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择 相比 L2正则化，L1正则化会产生更稀疏(sparse)的解。此处稀疏性指的是最优值中的一些参数为 0。和 L2正则化相比，L1正则化的稀疏性具有本质的不同。 - L2正则化 L2正则化是指权值向量w中各个元素的平方和然后再求平方根（可以看到Ridge回归的L2正则化项有平方符号），通常表示为$||w||_2$ L2正则化可以防止模型过拟合（overfitting）；一定程度上，L1也可以防止过拟合
L1正则化使得解稀疏，L2正则化通过使解趋近于0而不是等于0达到提升泛化能力的目的。
LR深入理解 关于LR的总结 其中包括了逻辑回归的相关问题，值得一看 机器学习算法与Python实践之（七）逻辑回归（Logistic Regression）
overfitting怎么解决？
- dropout 在第一种近似下，Dropout可以被认为是集成大量深层神经网络的使用Bagging方法。Dropout提供了一种廉价的Bagging集成近似，能够训练和评估指数级数量的神经网络。Bagging是一种集成方法，dropout相当于各个不同的集成共用一个模型进行了参数共享，一般作为分类器最后一层全联接之后，超参数一般取之为0.5。
- regularization 正则化 包括L2正则化、L1正则化
- bagging集成方法 Bagging(bootstrap aggregating)是通过结合几个模型降低泛化误差的技术 (Breiman, 1994)。主要想法是分别训练几个不同的模型，然后让所有模型表决测试样例的输出。这是机器学习中常规策略的一个例子，被称为模型平均(model averaging)。采用这种策略的技术被称为集成方法。
- batch normalization BN 批规范化，即在每次SGD时，通过mini-batch来对相应的activation做规范化操作，使得结果（输出信号各个维度）的均值为0，方差为1。 算法本质原理：在网络的每一层输入的时候，又插入了一个归一化层，也就是先做一个归一化处理，然后再进入网络的下一层。不过文献归一化层，可不像我们想象的那么简单，它是一个可学习、有参数的网络层。 使用变换重构，在不破坏上一层网络的特征分布的前提下进行归一化，引入了可学习参数γ、β，这就是算法关键之处，核心是先对原数据进行变化。
batch normation的原理
batch normation的BP
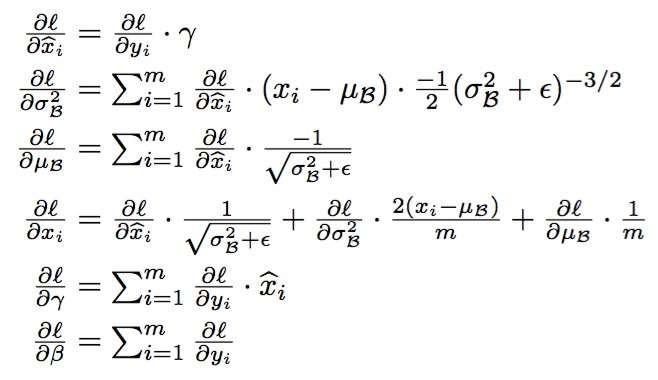
Implementation of Batch Normalization Layer 对Batch Normalization介绍较好
Deep Learning 之 batch normalization
- early stopping 即在每一个epoch结束时（一个epoch即对所有训练数据的一轮遍历）计算 validation data的accuracy，当accuracy不再提高时，就停止训练。这是很自然的做法，因为accuracy不再提高了，训练下去也没用。这样做能防止overfitting。
机器学习算法中如何选取超参数：学习速率、正则项系数、minibatch size
深度学习中 Batch Normalization为什么效果好？
在k-means或kNN，我们常用欧氏距离来计算最近的邻居之间的距离，有时也用曼哈顿距离，请对比下这两种距离的差别。
欧氏距离：
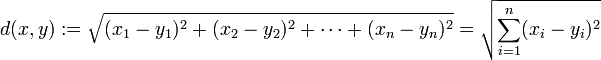曼哈顿距离：
LR和SVM的联系与区别
@朝阳在望，联系：
1、LR和SVM都可以处理分类问题，且一般都用于处理线性二分类问题（在改进的情况下可以处理多分类问题）
2、两个方法都可以增加不同的正则化项，如L1、L2等等。所以在很多实验中，两种算法的结果是很接近的。 区别： 1、LR是参数模型，SVM是非参数模型。 2、从目标函数来看，区别在于逻辑回归采用的是logistical loss对数损失函数（$\sum{-ylogP(y|x)}$），SVM采用的是hinge loss合叶函数$\sum_{i=1}^{N}[1-y_i(w xi +b)]+$，这个损失仅仅在正数的时候有损失，即outilers的情况损失。这两个损失函数的目的都是增加对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重。 3、SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减小了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。 4、逻辑回归相对来说模型更简单，好理解，特别是大规模线性分类时比较方便。而SVM的理解和优化相对来说复杂一些，SVM转化为对偶问题后,分类只需要计算与少数几个支持向量的距离,这个在进行复杂核函数计算时优势很明显,能够大大简化模型和计算。 5、logic 能做的 svm能做，但可能在准确率上有问题，svm能做的logic有的做不了。
softmax推导过程
softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解，从而来进行多分类！ 假设我们有一个数组，V，Vi表示V中的第i个元素，那么这个元素的softmax值就是 $$S_i=\frac{e_i}{\sum_j{e_j}}$$ softmax直白来说就是将原来输出是3,1,-3通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标！
softmax求导
要使用梯度下降，肯定需要一个损失函数，这里我们使用交叉熵作为我们的损失函数，为什么使用交叉熵损失函数，不是这篇文章重点，后面有时间会单独写一下为什么要用到交叉熵函数（这里我们默认选取它作为损失函数） $$Loss=-\sum_i{y_i \ln a_i}$$
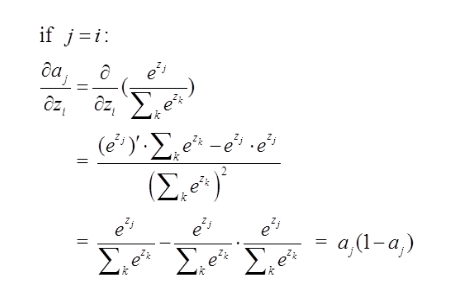
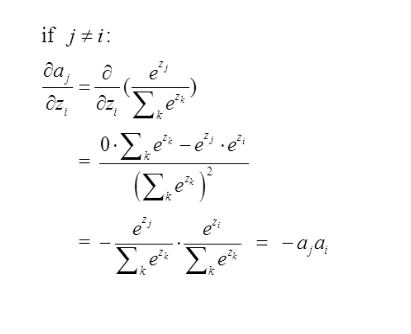
convolution实现
deconvolution实现
卷积过程如下
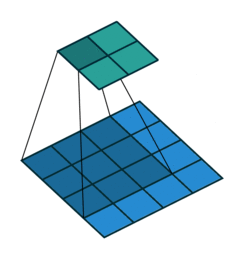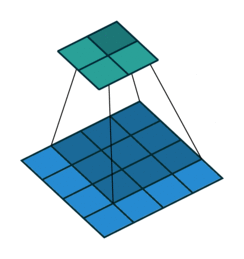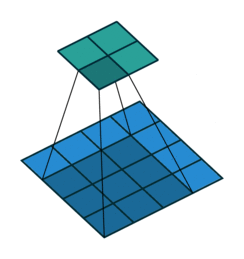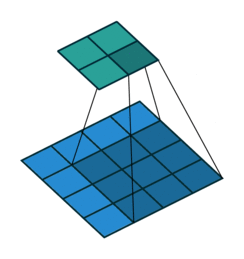
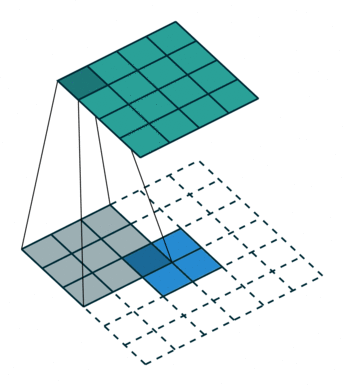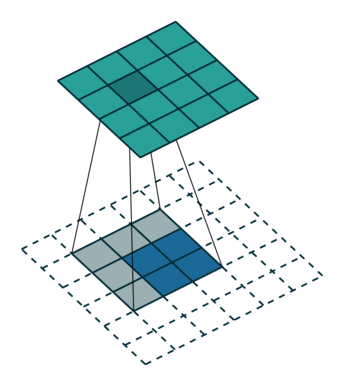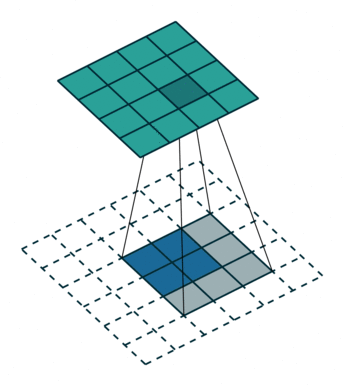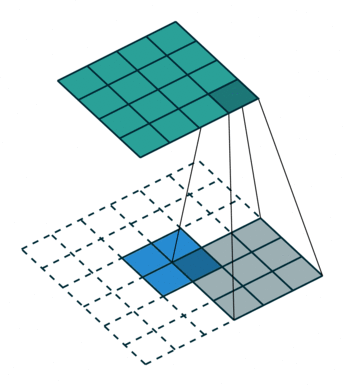
转置卷积过程如下，存在补0操作
深度学习卷积网络中反卷积/转置卷积的理解 transposed conv/deconv 如何理解深度学习中的deconvolution networks？
如何理解深度学习中的deconvolution networks？ - 知乎
转置卷积和卷积的对应关系可以理解为正向卷积为0 padding，那么转置卷积就是full padding。 公式关系为正向卷积s=1,p=0那么转置卷积的k’=k,s’=s,p’=k-1,转置卷积的输出尺寸
Transposed Convolution, Fractionally Strided Convolution or Deconvolution 本文讲解转置卷积最为清楚。
反向传播过程
BP算法的核心，是误差反向传播，通过递推式子计算每一层的误差（BP1-BP2），根据误差计算每一层参数的梯度（BP3-BP4）。
densenet实现
SGD 中 S(stochastic)代表什么
mini-batch和Full-batch，GD梯度下降指的是full-batch，而S随机梯度下降指的是mini-batch（设置batch_size）。
监督学习／迁移学习／半监督学习／弱监督学习／非监督学习？
- 监督学习：给定标签的训练集进行学习。
- 迁移学习：某一训练集训练的权值使用微调的方式作为另一个数据集的初始训练权值进行学习。
- 半监督学习：部分训练集有标签，大量训练集无标签。
- 弱监督学习：给定的标签不是完全对应于最后的标签，比如像素级分割学习，给定的标签仅仅是图像类别或者物体的bounding box，而不是最后的标签类别图。
- 非监督学习：无标签学习，比如聚类，KNN聚类等
激活函数
Sigmoid／Tanh（双曲正切函数）／ReLU以及ReLU线性整理的变种，比如PReLU和LReLU，解决了ReLU负半区神经死亡的问题
Sigmoid：
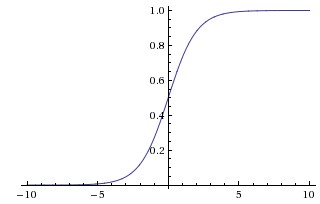- 缺点：会有梯度弥散、不是关于原点对称、计算exp比较耗时
- 优点：
Tanh：
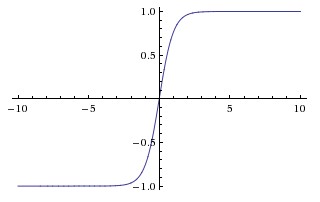- 缺点：梯度弥散没解决
- 优点：解决了原点对称问题、比sigmoid更快
ReLU：
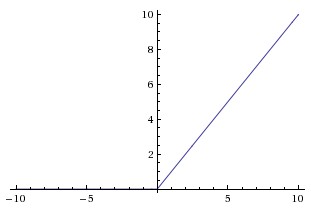- 缺点：梯度弥散没完全解决，在（-）部分相当于神经元死亡而且不会复活
- 优点：解决了部分梯度弥散问题、收敛速度更快
用过哪些DL的library呀?
pytorch、tensorflow、caffe、keras、thenao，这些DL库的优缺点。
现在的DL的state of art model有哪些呀?
2012 AlexNet 2013 ZFNet 2015 GoogLeNet 2016 ResNet 2017 DenseNet
如何pre-train model呀?
将模型在大的宽泛的数据集上训练，然后将该权值作为模型的初始权重加载。
损失函数
常见的损失函数Cross-Entropy / MSE／KL散度 其中KL散度和Cross-Entropy是信息论中的相关损失度量，KL散度的最小化等价于Cross-Entropy交叉熵的最小化，另外MSE是均方根最小误差。通常Cross-Entropy交叉熵损失函数应用在分类模型中，而MSE均方差误差应用在回归问题中。
机器学习算法系列（24）：机器学习中的损失函数 损失函数总结的非常好，值得根据这个目录进行总结。
CNN最成功的应用是在CV，那为什么NLP和Speech的很多问题也可以用CNN解出来？为什么AlphaGo里也用了CNN？这几个不相关的问题的相似性在哪里？CNN通过什么手段抓住了这个共性？
以上几个不相关问题的相关性在于，都存在局部与整体的关系，由低层次的特征经过组合，组成高层次的特征，并且得到不同特征之间的空间相关性。如下图：低层次的直线／曲线等特征，组合成为不同的形状，最后得到汽车的表示。
CNN抓住此共性的手段主要有四个：局部连接／权值共享／池化操作／多层次结构。
局部连接使网络可以提取数据的局部特征；权值共享大大降低了网络的训练难度，一个Filter只提取一个特征，在整个图片（或者语音／文本） 中进行卷积；池化操作与多层次结构一起，实现了数据的降维，将低层次的局部特征组合成为较高层次的特征，从而对整个图片进行表示。
什麽样的资料集不适合用深度学习?
- 数据集过小
- 数据集没有局部相关性
对所有优化问题来说, 有没有可能找到比現在已知算法更好的算法?
没有免费的午餐定理： 也就是说：对于所有问题，无论学习算法A多聪明，学习算法 B多笨拙，它们的期望性能相同。 但是：没有免费午餐定力假设所有问题出现几率相同，实际应用中，不同的场景，会有不同的问题分布，所以，在优化算法时，针对具体问题进行分析，是算法优化的核心所在。
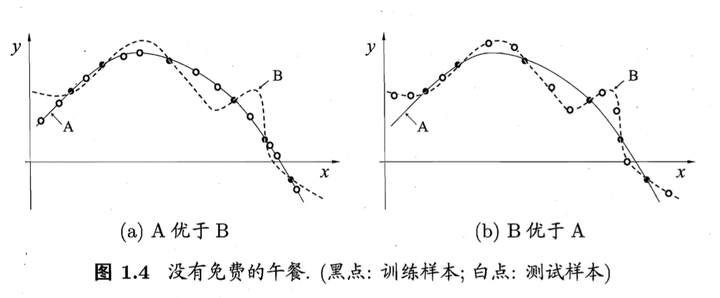
用贝叶斯机率说明Dropout的原理
TODO
什麽造成梯度消失问题? 推导一下
神经网络的训练中，通过改变神经元的权重，使网络的输出值尽可能逼近标签以降低误差值，训练普遍使用BP算法，核心思想是，计算出输出与标签间的损失函数值，然后计算其相对于每个神经元的梯度，进行权值的迭代。
梯度消失会造成权值更新缓慢，模型训练难度增加。造成梯度消失的一个原因是，许多激活函数将输出值挤压在很小的区间内，在激活函数两端较大范围的定义域内梯度为0。造成学习停止。常见的比如sigmoid函数，在x较大或较小时，梯度就很小了，而ReLU线性整流函数的导数不存在这种问题，它的导数除了0处为1。
梯度消失：这本质上是由于激活函数的选择导致的， 最简单的sigmoid函数为例，在函数的两端梯度求导结果非常小（饱和区），导致反向传播过程中由于多次用到激活函数的导数值使得整体的乘积梯度结果变得越来越小，也就出现了梯度消失的现象。考虑BP4，权值的更新依赖于激活函数的导数，如果激活函数的导数过小，梯度将更新缓慢甚至不在更新。
什麽造成梯度爆炸问题? 推导一下
出现在激活函数处在激活区，而且权重W过大的情况下。但是梯度爆炸不如梯度消失出现的机会多。
Weights Initialization. 不同的方式，造成的后果。为什么会造成这样的结果。
权值初始化 主要还是标准初始化作为一个最基本的模型，其中Xavier和He等初始化都是修改了正态初始化中的stdev和均匀分布中的scale，标准初始化即减均值，除标准差的z-score方法。 - 标准初始化 - 标准正态初始化 - 标准均匀初始化 - Xavier初始化 - Xavier正态初始化 - Xavier均匀初始化 - He初始化 - He正态初始化 - He均匀初始化
权值初始化的方法主要有：常量初始化、高斯分布初始化、positive-unitball初始化、均匀分布初始化、Xavier初始化、MSRA初始化、双线性初始化。
caffe中权值初始化方法 不仅介绍了权值初始化，同时也给出了caffe中的代码实现。
自动编码器
自编码器(autoencoder)是神经网络的一种，经过训练后能尝试将输入复制到输出。自编码器(autoencoder)内部有一个隐藏层h，可以产生编码(code)表示输入。该网络可以看作由两部分组成:一个由函数$h=f(x)$表示的编码器和一个生成重构的解码器$r=g(h)$。
如果一个自编码器只是简单地学会将处处设置为$g(f(x))=x$，那么这个自编码器就没什么特别的用处。相反，我们不应该将自编码器设计成输入到输出完全相等。这通常需要向自编码器强加一些约束，使它只能近似地复制，并只能复制与训练数据相似的输入。这些约束强制模型考虑输入数据的哪些部分需要被优先复制，因此它往往能学习到数据的有用特性。
自动编码器 介绍了各种不同的自动编码器，值得深入学习。
Deep Learning（深度学习）学习笔记整理系列之（四）
优化算法
TODO
RNN原理
在普通的全连接网络或CNN中，每层神经元的信号只能向上一层传播，样本的处理在各个时刻独立，因此又被成为前向神经网络(Feed-forward+Neural+Networks)。而在RNN中，神经元的输出可以在下一个时间戳直接作用到自身，即第i层神经元在m时刻的输入，除了（i-1）层神经元在该时刻的输出外，还包括其自身在（m-1）时刻的输出。所以叫循环神经网络。
类似于控制科学理论中的状态方程。
RNN、LSTM、GRU区别
RNN引入了循环的概念，但是在实际过程中却出现了初始信息随时间消失的问题，即长期依赖（Long-Term Dependencies）问题，所以引入了LSTM。 LSTM：因为LSTM有进有出且当前的cell informaton是通过input gate控制之后叠加的，RNN是叠乘，因此LSTM可以防止梯度消失或者爆炸。主要组件forget gate，input gate，cell state，GRU是LSTM的变体，将忘记门（forget gate）和输入门（input gate）合成了一个单一的更新门（update gate）。
LSTM防止梯度弥散和爆炸
LSTM用加和的方式取代了乘积，使得很难出现梯度弥散。但是相应的更大的几率会出现梯度爆炸，但是可以通过给梯度加门限解决这一问题。
xgboost
TODO 主要是随机森林中的应用，提升精度。
GAN
GAN结合了生成模型和判别模型，相当于矛与盾的撞击。生成模型负责生成最好的数据骗过判别模型，而判别模型负责识别出哪些是真的哪些是生成模型生成的。但是这些只是在了解了GAN之后才体会到的，但是为什么这样会有效呢？
机器学习中的Bias(偏差)，Error(误差)，和Variance(方差)有什么区别和联系？
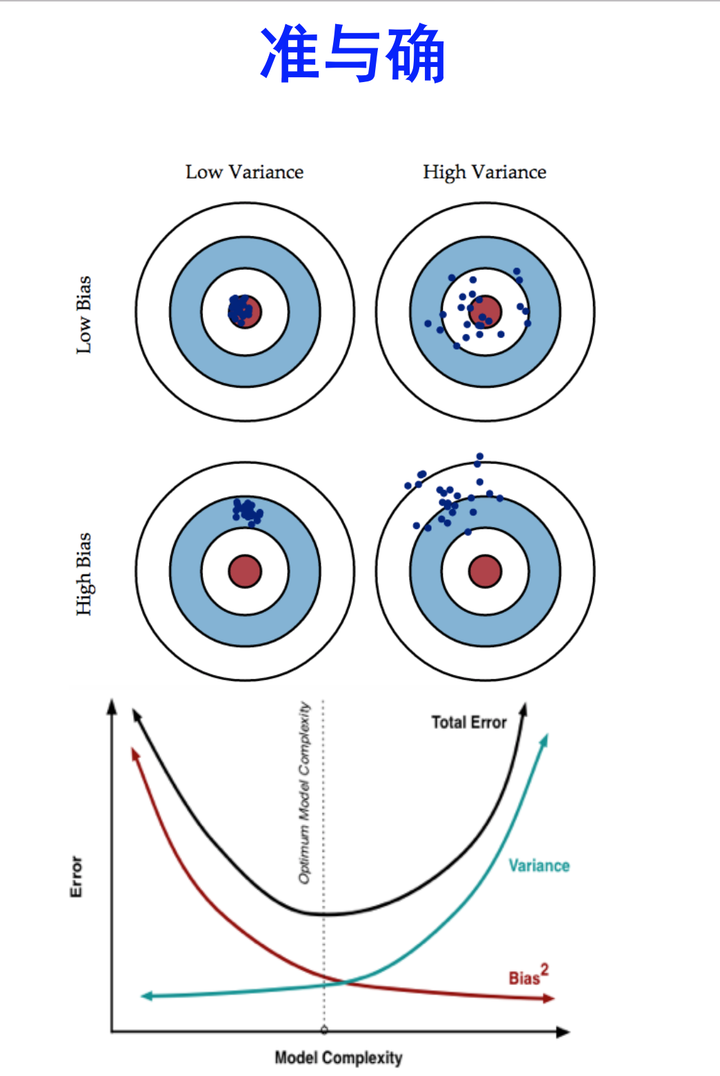
Error可以理解为在测试数据上跑出来的不准确率 ，即为 (1-准确率)。
在训练数据上面，我们可以进行交叉验证(Cross-Validation)。 一种方法叫做K-fold Cross Validation (K折交叉验证), K折交叉验证，初始采样分割成K个子样本，一个单独的子样本被保留作为验证模型的数据，其他K-1个样本用来训练。交叉验证重复K次，每个子样本验证一次，平均K次的结果或者使用其它结合方式，最终得到一个单一估测。
当K值大的时候， 我们会有更少的Bias(偏差), 更多的Variance。可以考虑为接近batch_size=1的情况，那么个体之间的方差肯定更大了，但是Bias会减小 当K值小的时候， 我们会有更多的Bias(偏差), 更少的Variance。可以考虑为几乎为full_batch_size进行切分，数据量大的情况下方差肯定小了，但是偏差会增加。
- K值大的时候，分割的样本数小，所以样本内的Bias小（样本之间的差距），样本间的Variance大。
- K值小的时候，分割的样本数大，所以样本内的Bias大（样本之间的差距），样本间的Variance小。
Error可以理解为在测试数据上跑出来的不准确率 ，即为 (1-准确率)。
当K值大的时候， 我们会有更少的Bias(偏差), 更多的Variance。 当K值小的时候， 我们会有更多的Bias(偏差), 更少的Variance。
想当然地，我们希望偏差与方差越小越好，但实际并非如此。一般来说，偏差与方差是有冲突的，称为偏差-方差窘境 (bias-variance dilemma)。
准确是两个概念。准是 bias 小，确是 variance 小。准确是相对概念，因为 bias-variance tradeoff。 ——Liam Huang
在机器学习领域，人们总是希望使自己的模型尽可能准确地描述数据背后的真实规律。通俗所言的「准确」，其实就是误差小。在领域中，排除人为失误，人们一般会遇到三种误差来源：随机误差、偏差和方差。偏差和方差又与「欠拟合」及「过拟合」紧紧联系在一起。由于随机误差是不可消除的，所以此篇我们讨论在偏差和方差之间的权衡（Bias-Variance Tradeoff）。
欠拟合 当模型处于欠拟合状态时，根本的办法是增加模型复杂度。我们一般有以下一些办法：
- 增加模型的迭代次数；
- 更换描述能力更强的模型；
- 生成更多特征供训练使用；
- 降低正则化水平。
过拟合 当模型处于过拟合状态时，根本的办法是降低模型复杂度。我们则有以下一些武器：
- 扩增训练集；
- 减少训练使用的特征的数量；
- 提高正则化水平。
均方误差为偏差的平方+协方差+随机误差，随机误差不可消除
偏差与方差 介绍偏差与方差较为清楚。
机器学习中的Bias(偏差)，Error(误差)，和Variance(方差)有什么区别和联系？
如何理解空洞卷积（dilated convolution）？
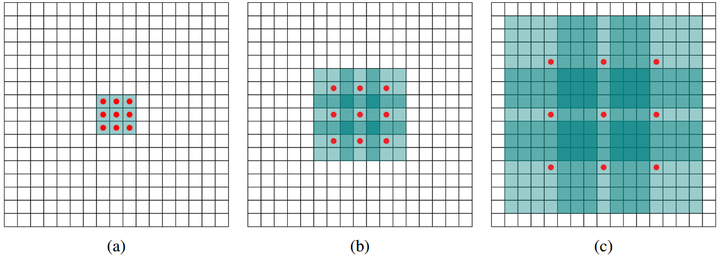
dilated的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。在图像需要全局信息或者语音文本需要较长的sequence信息依赖的问题中，都能很好的应用dilated conv，比如图像分割[3]、语音合成WaveNet[2]、机器翻译ByteNet[1]中。简单贴下ByteNet和WaveNet用到的dilated conv结构，可以更形象的了解dilated conv本身。
如何理解空洞卷积（dilated convolution）？
准确率(Accuracy), 精确率(Precision), 召回率(Recall)和F1-Measure
下面的表格表示了TP、FN、FP和TN的表示情况，其中斜对角线表示的都是True，而负对角线表示的是False，之后紧跟着的是预测情况是正例还是反例，如果预测结果是正例，同时是正确的，则表示为TP。
| 真实情况\预测情况 | 正例 | 反例 |
|---|---|---|
| 正例 | TP（真正例） | FN（假反例） |
| 反例 | FP（假正例） | TN（真反例） |
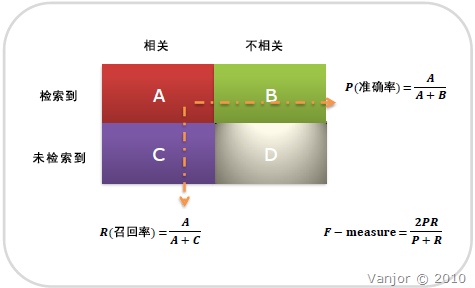
P、R表示精确率和召回率，如下所示： 精确率表示真实情况为正例的情况下，预测为正例的精度；召回率表示预测为正例的情况下，真实情况为正例的情况。
$$P=\frac{TP}{TP+FN}$$ $$R=\frac{TP}{TP+FP}$$ $$2/F1=1/P+1/R$$
准确率(Accuracy), 精确率(Precision), 召回率(Recall)和F1-Measure
Sigmoid 函数和 Softmax 函数的区别和关系
sigmoid函数
$$S(x)=\frac{1}{1+e^{-x}}$$
softmax函数
$$S(x_j)=\frac{e^{xj}}{\sum{k=1}^{N}{e^{x_k}}}$$
二元分类下，softmax函数退化为sigmoid函数
sigmoid为： $$P(y=0|x)=\frac{e^{w^T x+b}}{1+e^{w^T x+b}}$$ $$P(y=1|x)=\frac{1}{1+e^{w^T x+b}}$$
N=2，softmax为： $$P(y=1|x)=\frac{e^{w_1^T x+b_1}}{e^{w_1^T x+b_1}+e^{w_2^T x+b_2}}=\frac{1}{1+e^{(w_2 -w_1)^T x+(b_2-b_1)}}$$ $$P(y=0|x)=\frac{e^{w_2^T x+b_2}}{e^{w_1^T x+b_1}+e^{w_2^T x+b_2}}=\frac{e^{(w_2 -w_1)^T x+(b_2-b_1)}}{1+e^{(w_2 -w_1)^T x+(b_2-b_1)}}$$
如何通俗易懂地解释「协方差」与「相关系数」的概念？
总结：Bias(偏差)，Error(误差)，Variance(方差)及CV(交叉验证)
总结：Bias(偏差)，Error(误差)，Variance(方差)及CV(交叉验证)
机器学习中的Bias(偏差)，Error(误差)，和Variance(方差)有什么区别和联系？
相关面试总结资料
Deep Learning Interview 作者整理了深度学习面试的相关问题。